Buscar este blog
Facultad de Medicina, Universidad de Los Andes, Mérida, Venezuela
Facilitador Joan Fernando Chipia Lobo.
Entradas
Mostrando entradas de julio, 2012
Actitudes populares hacia la Estadística
- Obtener enlace
- Correo electrónico
- Otras aplicaciones
Indicador de salud
- Obtener enlace
- Correo electrónico
- Otras aplicaciones
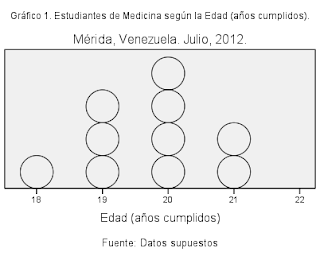
Gráfico de puntos y pictogramas
- Obtener enlace
- Correo electrónico
- Otras aplicaciones
Proporción, razón y tasa.
- Obtener enlace
- Correo electrónico
- Otras aplicaciones
Agrupamiento de datos cuantitativos
- Obtener enlace
- Correo electrónico
- Otras aplicaciones
Independencia de Venezuela
- Obtener enlace
- Correo electrónico
- Otras aplicaciones